蔡少棠教授或因准确预言忆阻器而获得诺贝尔奖

美国加州理工大学伯克利分校的物理学教授蔡少棠教授在三十年前根据对称性原理，准确地预言了第四元件--忆阻器的存在。所谓忆阻器，即是基本电路元件电阻，电感和电容这三种基本元件后的第四种。

忆阻器于去年被美国惠普公司的科学家发现。这个发现可以解释很多物理学和生物学上的未知现象。

其实，忆阻器存在于有机物中间，美国科学家已经证明单细胞和多细胞中均有忆阻器现象，可以推断的是，细胞单元的构成就是等效成忆阻器的构成。渔夫曾经断言，忆阻器的发现可以解释中医经络的存在。而最近美国科学家的工作似乎正在朝这个方向前进。已经从变形虫的模拟中看到基本生物体只需忆阻器的功能既可以生存。

渔夫经过思考认为，解释经络的存在可以利用忆阻器的原理，但渔夫尚不能解释气的运行，所以还有一个未知的东西在前面等着。等到把思考的结果整理后，可以写一篇相关的话题文章。

根据蔡少棠教授对物理学的贡献，渔夫以为给他一个诺贝尔奖也不算什么，要知道这可是彻底改变教科书的东西，就像当年牛顿发现第一定律一样（这可是蔡教授自己说的），让人对自然界的认识又调高了一个层次。

渔夫没有看到国内科研机构对此有任何反应，不知道是什么道理。但是在惠普公司的科学家团队中，有至少两个人是华裔的，因为他们都是中文名字。

渔夫估计要等到诺贝尔奖颁布后，大陆上一定会有一批人出来说自己也发现了忆阻器，就像当年超导现象一样，搞得闹剧一场。

这可不是愚人节的笑话！

无聊的山寨奥数练习（四）正方形（马赛克问题2）

一般而言，逆向运算总是烦一点，而且不一定有通用规律。当我们只有一个大正方形时，要画出它的2分之1或者3分之1或者10分之一面积的小正方形时，就只能就事论事，看菜下单了。不过，好在如果知道如何找2分之1，三分之一后，那么，六分之一就解决了。换句话说，最难的是把所有素数的方法找出来，剩下的就是分解因数了。左图中也画到13分之一.接下来的14，15，16都是直接可以在原来的图上接着画就可以了，几乎没有太大的难度，但17怎么做？就留给有兴趣的看客了。如果能看懂做法的话，后面就不是难事了，这种题目可以用来提高学生的兴趣，看看他们有没有办法找出来。

遇到素数时，通常要对一边进行等分，例如，图中的7，11，13都是这种情况。可以预见后面一定也会要这样做。

当找到一个小方块后，再要切割就容易了。可以用前面的方法，或者平移法倒推。

无聊的山寨奥数练习（三）正方形（马赛克问题）

从勾股定理衍生出的马赛克问题是一个有趣的问题，即如果有大小相等的小正方形若干，如何用最简单的方法将其拼成一个大正方形。最简单的拼法是用平移的办法，但这样拼出来的图形不美观。渔夫发现用一种所谓四叶包心的办法来拼图，看上去很有意思，在此和大家分享。我们从两个正方形开始，一直做到14个正方形。如果你仔细看过，就知道后面就是依样画葫芦了。

在图中，每个颜色代表一个小方块，这样就可以看出每个方块是如何被切割的。

如果把每个拼完的方块再拼起来，就是一副很好看的马赛克图案。如果把方块的颜色适当调整，（减少颜色）变得对称后，你会发现一些有趣的画面。

还有一个有趣的现象是，如果一个大正方形的数目是两个平方数的和，那么一定可以用这个大正方形直接套出一个拼接完整的图形。例如，5，10，13.，当然本身是平方数时，就是一个规整的正方形，例如4，9，16.

这里没有公布最简单的答案，例如3个小正方形可以切成六块拼出一个大正方形。

看完这个题目，还有一个问题，如果给定一个正方形，要把它分成n个小正方形，怎么办？下个帖子继续讨论。

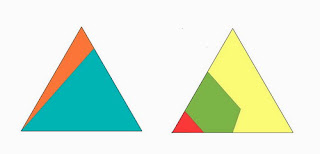
无聊的山寨奥数练习（二）三角形

三角形的拼接确实有些难度，渔夫一一说来。

第一种做法是把三角形拼成平行四边形，然后再把平行四边形变成大三角形要用的平行四边形，再变成三角形，这样的做法是7块。

第二种是利用任意两个正三角形拼接成一个大正三角形的做法，（该做法网上有）只是正好两个三角形全等，所以切割的块数可以少一些，是六块。

第三种是渔夫自创，可以切成5块，但其中的红色块要翻转一次。特别说明，S和T分别是AJ和AM的中点。渔夫认为不可能有再少的块数了，但却无法证明。哪位大师路过，给渔夫一个证明看看？

无聊的山寨奥数练习（一）长方形

渔夫尽管打渔为生，但闲来也看看奥数之类的无聊题目，作为休闲的一个部分。最近山寨文化流行，搞得渔夫心里痒痒，欲跟上时代潮流。故刻意做了几个无聊的奥数题。因为非科班出身，所以属于山寨。山寨现在是很光荣的事，想来想去，我们的伟大领袖毛主席不也是山寨出身吗？所以渔夫也就信心百倍地冲将出来，搞几个初中生的奥数题。不过看客千万不要给自己的小孩做，且当看笑话就是了。

问题1：将两个大小相等的等边三角形切割后合成一个等边三角形，怎样切割使被分割的块数最少？（切割后的形状可以任意翻转使用）。（答案：5）

问题2：将两个大小不同的相似的长方形（即两个长方形的长宽比一样）切割后合成一个相似的长方形，怎样切割使被分割的块数最少？（答案：5）

特别说明：即使不切割，也有2块。所以切割数是含有所有块数的。

先给出第2题的解：见右上图：

把一个长方形竖过来放，然后移来移去，得到BCD三个点，按照图中的方法连接就可以得到切割的曲线。

当然，如果把长方形变成正方形，就是勾股定理的证明了。不过渔夫提醒一下，这个做法本身是利用勾股定理的，所以不可以倒过来呀。但做法确实可以用。学过勾股定理的可以证明这个做法。渔夫这里就不证明了。最后拼成的长方形是ABCD。

因为这个帖子发图片不方便，所以关于三角形的答案在下一篇里发。

附加题：如果两个长方形是相等的，那么最少切几块呢？

另外，上面的结论是不是一直成立呢？如果有问题的话，什么情况下有问题？例如长宽比发生变化时。