生长中的数学原理

由于谷歌的博客排版功能太烂，只能将就着写这篇插图很多的博客了。

因为研究经络问题，不可避免地要遇到细胞增长问题，所以一直又研究生长的问题，一直想看那本生长和形态，但还没有到手，所以自己先做一些功课。有了一些心得，录在这里：

1.任意矩形的生长

曾经看过鹦鹉螺曲线的做法，很受启发，结果往下在仔细研究，发现只要是任意矩形，按照最长边原则（即总是在多的一面生长）生长正方形的话，也能得到同样的结果，所以又推导一下，很容易就获得图1 的结果。结论是，只要有生长，就有黄金比。这是自然界的数学原理，所以我们会到处遇到。

2.生长的不同模式

在看了鹦鹉螺曲线后，我又在思考如果每次长的正方形是两个，会怎样，三个，或者n个呢？

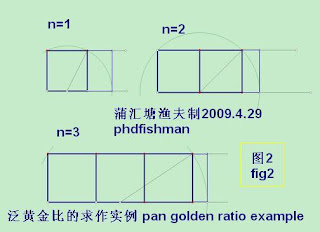
见图4.结果发现它们也会有相似性存在，也就是说，在生长到一定阶段后，后面的矩形一定和前面的相似。最后一定有一个矩形满足一个特定的比。用几何作图法很容易求出每次生长n个正方形的矩形。图2列出了前3种做法。

3.泛黄金比（广义黄金律）

用简单数学方法很容易获得对于每次生长n个正方形的比例公式，图3列出了前面19个的数据。可以看出，日常的黄金律只是一个特例，因为n=1是最容易生长的一种方式，所以在自然界中最容易被我们观察到。我相信我们的身上到处都是这些黄金比，只是过去没有注意罢了。

4.帕特农神庙里的比例

最近看到一个片子，讲希腊帕特农神庙里的比例问题。人们已经发现长宽比的黄金比，但对于柱子高度和间隔长度的比，现代希腊人认为是4：9，但我认为就应该是0.414.现在还没有拿到具体数据，等以后验证吧。我相信古希腊人可能很早就注意到泛黄金比，只是没有写下来罢了。

我坚信一切生物都是按照最简单的数学原理和物理原理来生长的，进化论只是一个表象。因为任何细胞的生长都是依靠其忆阻特性（也就是其基本物理特性）来生长的，越简单的数学方式越容易用在低级细胞的生长上，而高级生物不过就是这些多种生长方式的组合和排列。但由于数量太过巨大，以至于人们根本无暇去看透他们的规律。有了电脑帮忙，现在有机会一点点找出规律来了。